[Solution] BOJ 23242

BOJ 백준 23242 Histogram

문제: https://www.acmicpc.net/problem/23242

길이가 $n$인 수열을 $B$개의 bucket으로 나누었을 때, 각 bucket의 $(오차)^2$ 합의 최솟값을 구하는 것이 문제이다.

여기서 말하는 오차는 $i$번째 원소의 $f$ 값에서 그 원소가 속한 bucket의 $f$ 값의 평균을 뺀 것을 뜻한다. 또한 $i$번째 원소의 $f$ 값은 리스트에서 $i$ 값이 나온 빈도를 의미하는데, 빈도 자체는 문제에서 크게 의미가 있지 않아서 $i$번째 원소의 어떠한 값이라고 이해해도 무관하다.

2021 ICPC Seoul Regional 예선에 출제되었던 문제이고, 실제로 대회에서 시간복잡도가 O(n²B)인 풀이법으로 이 문제를 해결했다. 그런데 지금 와서 보니 대회 때 생각했던 풀이보다 더 시간복잡도를 줄일 수 있는 방법이 있을 것 같다.

$n$의 제한이 4,000이고 $B$의 제한이 30 이므로 Dynamic Programming을 사용하여 $O(n^2B)$인 방법으로 해결해도 시간 제한 3초 안에 해결 가능할 것으로 판단하여 이를 택했는데, 시간 제한이 1초였으면 결과가 달라졌을지도 모른다. 여하튼 이 글에서는 $O(n^2B)$의 풀이로 포스팅하고자 한다.

다음과 같이 메모이제이션할 배열을 정의했다.

$dp[i][j]$: $i$번째 원소까지 본 상태에서 $j$개의 bucket으로 나누었을 때 최소 $(오차)^2$ 합

$dp[i][j]$를 계산하려면 i번째보다 앞에 있는 원소까지 봤고 그 때 $j-1$개의 bucket으로 나누었을 때의 최소 $(오차)^2$ 합에다가 그 이후부터 $i$번째 원소까지 새로 생기는 $j$번째 bucket의 $(\text{오차})^2$ 합을 더한 값 중에서 가장 작은 것을 반영해주면 된다. 점화식을 정리하면 다음과 같다.

$∑(Error)^2$: $k+1$ 부터 $i$ 번째까지의 $(\text{오차})^2$ 합

그런데 시간복잡도를 고려할 때 $∑(Error)^2$ 값을 구하는 부분에서 또 loop를 시행할 수는 없으므로 $dp$ 배열 값을 구하기 전에 필요한 데이터를 미리 계산해 놓아야 한다. 그래서 각 원소의 누적합을 저장하는 sum 배열과 제곱에 대한 누적합을 갖는 expo 배열을 선언했는데, 이렇게 두 배열을 정의한 이유는 $∑(Error)^2$ 정리식에 관한 필기 노트를 참고하면 알 수 있다.

$sum[i]$: 첫 번째부터 $i$번째 원소까지의 $f$ 값의 누적 합

$expo[i]$: 첫 번째부터 $i$번째 원소까지의 $f^2$ 값의 누적 합

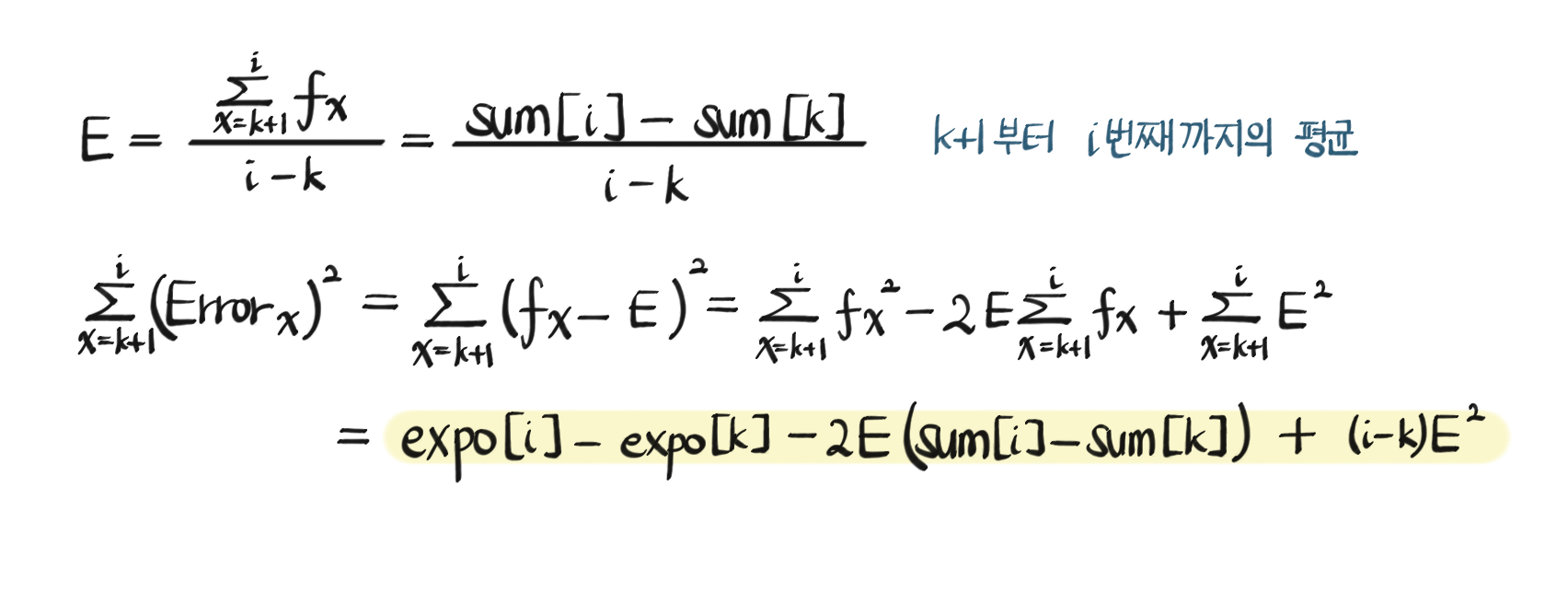
\(E = ∑\frac{f}{i - k} = \frac{sum[i] - sum[k]}{i - k}\)

\(\begin{align} ∑(Error)^2 &= ∑(f - E)^2 \\&= ∑f^2 - 2E∑f + ∑E^2 \\&= expo[i] - expo[k] - 2E(sum[i] - sum[k]) + (i - k)E^2 \end{align}\)

코드를 보면 이해가 더 빠를 것이다.

#include <iostream>
#include <algorithm>
using namespace std;

const double INF = (double)(1e12 * 4);
const int N_MAX = 4000;
const int B_MAX = 30;

int b, n;
double sum[N_MAX + 1];
double expo[N_MAX + 1];
double dp[N_MAX + 1][B_MAX + 1];

int main(){
    cin.tie(NULL);
    cin.sync_with_stdio(false);
    
    cin >> b >> n;
    
    for (int i = 1; i <= n; i++){
        double x; cin >> x;
        sum[i] = sum[i - 1] + x;
        expo[i] = expo[i - 1] + x * x;
        for (int j = 0; j <= b; j++){
            dp[i][j] = INF;
        }
    }
    
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= b; j++){
            for (int k = 0; k < i; k++){
                if (dp[k][j - 1] == INF)
                    continue;
                double avg = (sum[i] - sum[k]) / (double)(i - k);
                double error = (expo[i] - expo[k]) - 2 * avg * (sum[i] - sum[k]) + avg * avg * (double)(i - k);
                dp[i][j] = min(dp[i][j], dp[k][j - 1] + error);
            }
        }
    }
    
    cout << fixed;
    cout.precision(6);
    cout << dp[n][b] << "\n";
    
    return 0;
}